Все, что нужно знать о треугольнике. Первый признак равенства треугольников: формулировка и доказательство (7 класс) Что такое 1 признак равенства треугольников

В этой статье мы расскажем, как можно сформулировать и доказать первый признак равенства треугольников , который проходят в 7 классе.

Формулировка первого признака равенства треугольников

«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по двум сторонам и углу между ними».

Прежде чем перейти к необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.

Что такое треугольник и когда они считаются равными?

Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами ).

На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.

Рисунок 1

Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными ). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.

Доказательство первого признака равенства треугольников

Дано:

Два треугольника: ABC и DEF (рисунок 2).

Рисунок 2

По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).

Доказать , что треугольник ABC равен треугольнику DEF.

Доказательство:

Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.

Теорема доказана.

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы,срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольномтреугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые (рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21), то это прямоугольный треугольник ; стороны a , b , образующие прямой угол, называются катетами ; сторона c , противоположная прямому углу, называется гипотенузой . Если один из углов тупой ( B, рис.22), то это тупоугольный треугольник.

Треугольник ABC (рис.23) - равнобедренный , если две его стороны равны (a = c ); эти равные стороны называются боковыми , третья сторона называется основанием треугольника. Треугольник ABC (рис.24) – равносторонний , если все его стороны равны (a = b = c ). В общем случае (a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний

угол BCD. Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B.

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности (a < b + c , a > b – c ;b < a + c , b > a – c ;c < a + b ,c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O , рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O , рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника (AD , BE , CF , рис.28) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника (AD , BE , CF , рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС (KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга (точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

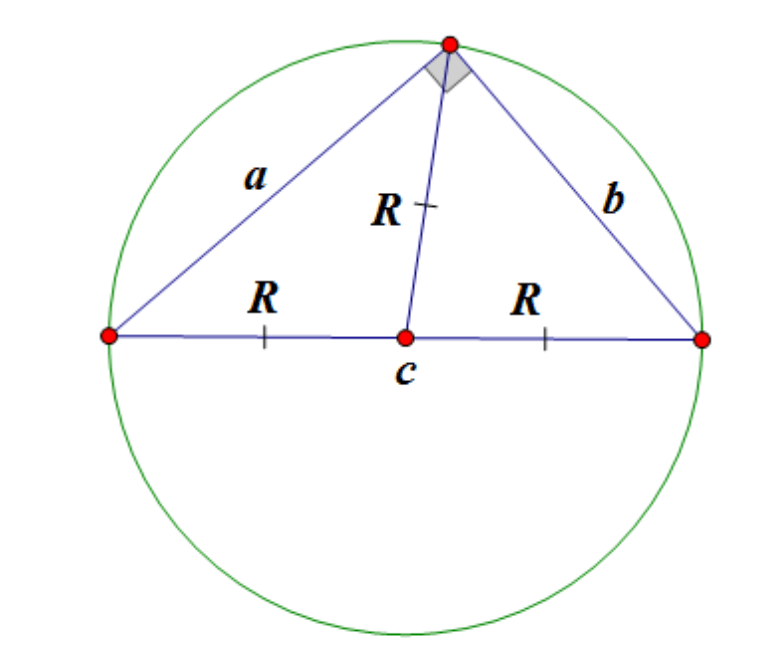
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна (a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

c 2 + 4 (ab / 2) = c 2 + 2 ab ,

отсюда ,

c 2 + 2 ab = (a + b ) 2 ,

и окончательно имеем:

c 2 = a 2 + b 2 .

Соотношение сторон в произвольном треугольнике.

В общем случае (для произвольного треугольника) имеем:

c 2 = a 2 + b 2 – 2ab · cos C,

где C – угол между сторонами a и b .

Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А 1 В 1 С 1 . Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.

Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.

Так, например, в равных треугольниках ABC и A 1 B 1 C 1 , изображенных на рисунке 1, против соответственно равных сторон АВ и А 1 В 1 лежат равные углы С и С 1 . Равенство треугольников ABC и А 1 В 1 С 1 будем обозначать так: Δ ABC = Δ А 1 В 1 С 1 . Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.

Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).

Доказательство. Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 (см. рис.2). Докажем, что Δ ABC = Δ A 1 B 1 C 1 .

Так как ∠ А = ∠ А 1 , то треугольник ABC можно наложить на треугольник А 1 В 1 С 1 так, что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и A 1 C 1 . Поскольку АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 а сторона АС - со стороной А 1 C 1 ; в частности, совместятся точки В и В 1 , С и C 1 . Следовательно, совместятся стороны ВС и В 1 С 1 . Итак, треугольники ABC и А 1 В 1 С 1 полностью совместятся, значит, они равны.

Аналогично методом наложения доказывается теорема 2.

Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).

Замечание. На основе теоремы 2 устанавливается теорема 3.

Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.

Из последней теоремы вытекает теорема 4.

Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны ().

Пример 1. В треугольниках ABC и DEF (рис. 4)

∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Сравнить треугольники ABC и DEF. Какой угол в треугольнике DEF равен углу В?

Решение. Данные треугольники равны по первому признаку. Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.

Пример 2. Отрезки АВ и CD (рис. 5) пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС равен 6 м?

Решение. Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные), АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.

При решении геометрических задач полезно следовать такому алгоритму. Во время чтения условия задачи необходимо

Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
Нанести все данные из условия задачи на чертеж
Выписать все геометрические понятия, которые встречаются в задаче
Вспомнить все теоремы, которые относятся к этим понятию
Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем

Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.

В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.

ТРЕУГОЛЬНИК.

Площадь треугольника.

1. ,

здесь - произвольная сторона треугольника, - высота, опущенная на эту сторону.

2. ,

здесь и - произвольные стороны треугольника, - угол между этими сторонами:

3. Формула Герона:

Здесь - длины сторон треугольника, - полупериметр треугольника,

4. ,

здесь - полупериметр треугольника, - радиус вписанной окружности.

Пусть - длины отрезков касательных.

Тогда формулу Герона можно записать в таком виде:

6. ,

здесь - длины сторон треугольника, - радиус описанной окружности.

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Медиана треугольника

Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

Радиус описанной окружности в два раза больше радиуса вписанной окружности: R=2r

Длина медианы произвольного треугольника

здесь - медиана, проведенная к стороне , - длины сторон треугольника.

Биссектриса треугольника

Это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:

Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.

Все точки биссектрисы угла равноудалены от сторон угла.

Высота треугольника

Это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Чтобы найти высоту треугольника , проведенную к стороне , нужно любым доступным способом найти его площадь, а затем воспользоваться формулой:

Центр окружности, описанной около треугольника , лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

Радиус описанной окружности треугольника можно найти по таким формулам:

Здесь - длины сторон треугольника, - площадь треугольника.

где - длина стороны треугольника, - противолежащий угол. (Эта формула вытекает из теоремы синусов).

Неравенство треугольника

Каждая сторона треугольника меньше суммы и больше разности двух других.

Сумма длин любых двух сторон всегда больше длины третьей стороны:

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:

Если , то и наоборот.

Теорема синусов:

стороны треугольника пропорциональны синусам противолежащих углов:

Теорема косинусов:

квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

Прямоугольный треугольник

- это треугольник, один из углов которого равен 90°.

Сумма острых углов прямоугольного треугольника равна 90°.

Гипотенуза - это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.

Теорема Пифагора:

квадрат гипотенузы равен сумме квадратов катетов :

Радиус окружности, вписанной в прямоугольный треугольник, равен

здесь - радиус вписанной окружности, - катеты, - гипотенуза:

Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:

Медиана прямоугольного треугольника, проведенная к гипотенузе , равна половине гипотенузы.

Определение синуса, косинуса, тангенса и котангенса прямоугольного треугольника смотрите

Соотношение элементов в прямоугольном треугольнике:

Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:

Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

Катет, лежащий против угла равен половине гипотенузы:

Равнобедренный треугольник.

Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.

В равнобедренном треугольнике углы при основании равны.

Угол при вершине.

И - боковые стороны,

И - углы при основании.

Высота, биссектриса и медиана.

Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.

Правильный треугольник

(или равносторонний треугольник ) - это треугольник, все стороны и углы которого равны между собой.

Площадь правильного треугольника равна

где - длина стороны треугольника.

Центр окружности, вписанной в правильный треугольник , совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.

Средняя линия треугольника

Это отрезок, соединяющий середины двух сторон.

На рисунке DE - средняя линия треугольника ABC.

Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE

Внешний угол треугольника

Это угол, смежный какому либо углу треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Тригонометрические функции внешнего угла:

Признаки равенства треугольников:

1 . Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.

Признаки подобия треугольников:

1 . Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.

2 . Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.

3 . Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.

Важно: в подобных треугольниках сходственные стороны лежат против равных углов.

Теорема Менелая

Пусть прямая пересекает треугольник , причем – точка ее пересечения со стороной , – точка ее пересечения со стороной , и – точка ее пересечения с продолжением стороны . Тогда

Билет 2

Вопрос 1

Признаки равенства треугольников (доказательство всех)

1-ый признак равенства треугольников: по двум сторонам и углу между ними (Теорема 3.1. – Признак равенства треугольников по двум сторонам и углу между ними - Если две стороны и угло между ними одного треугольнгрка равны соотвественно двум сторонам и углу между ними другого треугольника, то такие треугольники равны )

Доказательство:

Пусть у треугольников АВС и А 1 В 1 С 1 угол А равен углу А 1 , АВ равно А 1 В 1, АС равно А 1 С 1 , докажем, что треугольники равны.

Так как А 1 В 1 равно А 1 В 2 , то вершина В 2 совпадет с В 1. Так как угол В 1 А 1 С 1 равен углу В 2 А 1 С 2, то луч А 1 С 2 совпадет с А 1 С 1 . Так как А 1 С 1 равен А 1 С 2 , то С 2 совпадет с С 1. Значит треугольник А 1 В 1 С 1 совпадает стреугольниом А 1 В 2 С 2 , значит равен треугльнику АВС.

Теорема доказана.

2-ой признак равенства треугольников: по стороне и прилежим к ней углам (Теорема 3.2. - Признак равенства треугольников по стороне и прилежащим к ней углам - Если сторона и прилежащие у ней углы одного треугольника равны соотвественно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А 1 В 1 С 1 – два треугольника, у которых АВ равно А 1 В 1, угол А равен углу А 1 , и угол В равен углу В 1 . Докажем, что они равны.

Пусть А 1 В 2 С 2 – треугольник, равный АВС, с вершины В 2 на луче А 1 В 1 и вершины С 2 в той же полуплоскости относительно прямой А 1 В 1 , где лежит вершина С 1 .

Так как А 1 В 2 равно А 1 В 1 , то вершина В 2 совпадет с В 1. Так как угол В 1 А 1 С 2 равен углу В 1 А 1 С 1, и угол А1В1С2 равен углу А1В1С1, то луч А 1 С 2 совпадет с А 1 С 1 , а В 1 С 2 совпадет с В 1 С 1 . Отсюда следует, что вершина С 2 совпадет с С 1. Значит треугольник А 1 В 1 С 1 совпадает стреугольниом А 1 В 2 С 2 , значит равен треугльнику АВС.

Теорема доказана.

3-ий признак равенства треугольников: по трем сторонам (Теорема 3.6. - Признак равенства треугольников по трем сторонам - Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А 1 В 1 С 1 – два треугольника, у которых АВ равно А 1 В 1, АС равно А 1 С 1 , и ВС равно В 1 С 1 . Докажем, что они равны.

Допустим, треугольники не равны. Тогда у них угол А не равен углу А 1 , угол В не равен углу В 1, и угол С не равен углу С 1 . Иначе они были бы равны, по перовому признаку.

Пусть А 1 В 1 С 2 – треугольник, равный треугольнику АВС, у которого Свершина С 2 лежит в одной полуплоскости с вершиной С 1 относительно прямой А 1 В 1 .

Пусть D – середина отрезка С 1 С 2 . Треугольники А 1 С 1 С 2 и В 1 С 1 С 2 – равнобедренные с общим основанием С 1 С 2 . Поэтому их медианы А 1 D и В 1 D – являются высотами, значит прямые А 1 D и В 1 D – перпендикулярны прямой С 1 С 2. Прямые А 1 D и В 1 D не совпадают, так как точки А 1, В 1 , D не лежат на одной прямой, но через точку D прямой С 1 С 2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.