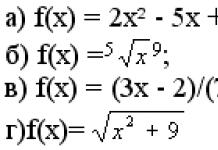Уравнение касательной к графику функции открытый урок. Конспект урока "Физический и геометрический смысл производной. Касательная к графику функции". История появления производной

Разделы: Математика

Цели.

• Обобщить и систематизировать правила дифференциирования;
• Повторить алгоритм построение касательной к графику функции, схему исследования функции;
• Решение задач на применение наибольшего и наименьшего значения функции.

Оборудование. Плакат “Производная. Правила вычисления производных. Применения производной”.

Ход урока

По картам у учащихся повторение теоретического материала.

1. Дайте определение производной функции в точке. Что называется дифференциированием? Какую функцию называют дифференциируемой в точке?

(Производной функции f в точке х называется число, к которому стремится отношение

Функцию, имеющую производную в точке х 0 , называют дифференциируемой в этой точке. Нахождение производной f называется дифференциированием.)

2. Сформулируйте правила нахождения производной.

(1. Производная суммы (u + v)"=u"+v";
2. О постоянном множителе (Cu)"=Cu";
3. Производная произведения (uv)"=u"v+uv";
4. Производная дроби (u/v)"=(u"v-uv")/v 2 ;
5. Производная степенной функции (x n)"=nx n+1 .)

3. Чему равны производные следующих функций:

4. Как найти производную сложной функции?

(Надо последовательно представить ее в виде элементарных функций и взять производную по известным правилам).

5. Чему равны производные следующих функций:

6. В чем заключается геометрический смысл производной?

(Существование производной в точке эквивалентно существованию невертикальной касательной в точке (х 0 ,f(x 0)) графика функции, причем угловой коэффициент этой касательной равен f "(x 0)).

7. Какой вид имеет уравнение касательной к графику функции в точке (x 0 ,f(x 0))?

(Уравнение касательной имеет вид у=f(x 0)+f"(x 0)(x-х 0))

8. Сформулируете алгоритм построения графика функции с помощью производной.

(1. Найти ООФ.
2. Исследовать на четность.
3. Исследовать на периодичность.
4. Найти точки пересечения графика с осями координат.
5. Найти производную функции и ее критические точки.
6. Найти промежутки монотонности и экстремумы функции.
7. Построить таблицу по результатам исследования.
8. Построить график функции.)

9. Сформулировать теоремы, с помощью которых модно построить график функции.

(1. Признак возрастания (убывания).
2. Необходимый признак экстремума.
3. Признак максимума (минимума).)

10. Какие формулы существуют для приближенных вычислений функций?

Индивидуальная работа.

Уровень А (три варианта), уровень Б (один вариант).

Уровень А.

Вариант 1.

1. Запишите уравнение касательной к графику функции

f(x)=(x -1) 2 (x -3) 3 параллельной прямой у=5-24х.

2. Число 18 педставьте в виде суммы трех положительных слагаемых так, чтобы одно слагаемое было в два раза больше другого, а произведение всех трех слагаемых было наибольшим.

4. Найдите промежутки возрастания и убывания функции f(x)=(x-1) e х+1 .

Вариант 2.

1. Под каким углом к оси абсцисс наклонена касательная к графику функции f(x)=0,x 2 +x-1,5 в точке с абсциссой х 0 = - 2? Напишите уравнение этой касательной и выполните рисунок к этой задаче.

2. Как в В. 1.

3. Найдите производную функции:

Уровень Б.

1. Найдите производную функции:

а) f(x) = e -5х;
б) f(x) = log 3 (2x 2 -3x+1).

2. Напишите уравение касательной к графику функции в точке с абсциссой х 0 , если f(x)=e -х, х 0 = 1.

3. Найдите промежутки возрастания и убывания функции f(x)=x·e 2х.

Итог урока.

Проверяется работа, выставляется отметка за теорию и практику.

Домашнее задание дается индивидуально:

а)повторить производные тригонометрических функций;
б)метод интервалов;
в)механический смысл производной.

2. А: №138, №142, Б: №137(а,б), №140(а).

3. Возмите производную функций:

а) f(x)=x 4 -3x 2 -7;
б) f(x)=4x 3 -6x;
в) f(x)=-2sin(2x-4);
г) f(x)=cos(2x-4).

4. Назовите схему исследования функции.

Дата: _____________________

Тема урока: Физический и геометрический смысл производной. Касательная к графику функции.

Тип урока: урок изучения нового материала.

Цели урока:

Учащиеся должны знать :

что называется угловым коэффициентом прямой;

углом между прямой и осью Ох;

в чем состоит геометрический смысл производной;

уравнение касательной к графику функции;

способ построения касательной к параболе;

уметь применять теоретические знания на практике.

Задачи урока :

Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями механический и геометрический смысл производной.

Воспитательные: формировать у учащихся научное мировоззрение.

Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.

Методы организации учебно-познавательной деятельности:

наглядные;

практические;

по мыслительной деятельности: индуктивный;

по усвоению материала: частично-поисковый, репродуктивный;

стимулирующие: поощрения;

контроля: устный фронтальный опрос.

План урока

Устные упражнения (найти производную)

Изучение нового материала

Решение заданий.

Подведение итогов урока.

Оборудование : карточки

Ход урока

“Человек лишь там чего – то добивается, где он верит в свои силы”

Л. Фейербах

I. Организационный момент.

Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.

Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.

Устный счет

1. Найдите производные:

", ()" , (4sin x)", (cos2x)", (tg x)", "

2. Логический тест.

а) Вставить пропущенное выражение.

II. Изучение нового материала.

Пойдем по пути Ньютона и Лейбница и посмотрим, каким способом можно анализировать процесс, рассматривая его как функцию времени.

Введем несколько понятий, которые помогут нам в дальнейшем.

Графиком линей ной функции y=kx+ b является прямая, число k называют угловым коэффициентом прямой k=tg, где – угол прямой, то есть угол между этой прямой и положительным направлением оси Ох.

Рисунок 1

Рассмотрим график функции у=f(х). Проведем секущую через любые две точки, например, секущую АМ. (Рис.2)

Угловой коэффициент секущей k=tg. В прямоугольном треугольнике АМС (объясните почему?). Тогда tg = = , что с точки зрения физики есть величина средней скорости протекания любого процесса на данном промежутке времени, например, скорости изменения расстояния в механике.

Рисунок 2

Рисунок 3

Сам термин “скорость” характеризует зависимость изменения одной величины от изменения другой, и последняя необязательно должна быть временем.

Итак, тангенс угла наклона секущей tg = .

Нас интересует зависимость изменения величин в более короткий промежуток времени. Устремим приращение аргумента к нулю. Тогда правая часть формулы – производная функции в точке А (объясните почему). Если х – 0, то точка М движется по графику к точке А, значит прямая АМ приближается к некоторой прямой АВ, которая является касательной к графику функции у = f(х) в точке А . (Рис.3)

Угол наклона секущей стремится к углу наклона касательной.

Геометрический смысл производной состоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в точке.

Механический смысл производной.

Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, то есть новая характеристика изучаемого процесса. Эту величину Лейбниц назвал производной , а Ньютон говорил, что производной называется сама мгновенная скорость .

III. Решение заданий.

Показать на доске.

Угловой коэффициент касательной к кривой f(х) = х 3 в точке х 0 – 1 есть значение производной этой функции при х = 1. f’(1) = 3х 2 ; f’(1) = 3.

№ 159, № 161 – у доски.

Вопросы к классу:

Каков физический смысл производной перемещения? (Скорость).

Можно ли найти производную скорости? Используется ли эта величина в физике? Как она называется? (Ускорение).

Мгновенная скорость равна нулю. Что можно сказать о движении тела в это момент? (Это момент остановки).

Каков физический смысл следующих высказываний: производная движения равна нулю в точке t 0; при переходе через точку t 0 производная меняет знак? (Тело останавливается; меняется направление движения на противоположное).

IV. Подведение итогов урока

1) В чем состоит геометрический смысл производной?
2) В чем состоит механический смысл производной?

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый.

Цель урока:

1. Ввести понятие касательной к графику функции в точке, выяснить, в чём состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
2. Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
3. Выработка коммуникативных навыков в работе, способствовать развитию самостоятельной деятельности учащихся.

Оборудование: компьютер, мультимедийный проектор, раздаточный материал.

Скачать:

Предварительный просмотр:

Урок по теме "Касательная. Уравнение касательной"

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый.

Цель урока:

1. Ввести понятие касательной к графику функции в точке, выяснить, в чём состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
2. Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
3. Выработка коммуникативных навыков в работе, способствовать развитию самостоятельной деятельности учащихся.

Оборудование: компьютер, мультимедийный проектор, раздаточный материал.

План урока

I Организационный момент.
Проверка готовности учащихся к уроку. Сообщение темы и девиза урока.

II Актуализация материала.
(Активизировать внимание, показать недостаточность знаний о касательной, сформулировать цели и задачи урока.)

Давайте обсудим, что такое касательная к графику функции? Согласны ли вы с утверждением, что «Касательная – это прямая, имеющая с данной кривой одну общую точку»?
Идёт обсуждение. Высказывания детей (да и почему, нет и почему). В процессе обсуждения приходим к выводу, что данное утверждение не верно.

Примеры.
1) Прямая x = 1 имеет с параболой y = x2 одну общую точку M(1; 1), однако не является касательной к параболе. Прямая же y = 2x – 1, проходящая через ту же точку, является касательной к данной параболе.
2) Аналогично, прямая x = π не является касательной к графику y = cos x , хотя имеет с ним единственную общую точку K(π; 1). С другой стороны, прямая y = - 1, проходящая через ту же точку, является касательной к графику, хотя имеет с ним бесконечно много общих точек вида; (π+2 πk; 1), где k – целое число, в каждой из которых она касается графика.

Постановка цели и задачи перед детьми на уроке: выяснить, что такое касательная к графику функции в точке, как составить уравнение касательной?
Что нам для этого понадобиться?
Вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной, правила дифференцирования.

III Подготовительная работа к изучению нового материала.
Опрос материала по карточкам: (задания выполняются на доске)
1 ученик: заполнить таблицу производных элементарных функций

2 ученик: вспомни правила дифференцирования

3 ученик: составьте уравнение прямой y = kx + 4 , проходящей через точку А(3; -2).
(y = -2x+4)

4 ученик: составьте уравнение прямей y = 3x + b , проходящей через точку С(4; 2).
(y = 3x – 2).

С остальными фронтальная работа.

1. Сформулируйте определение производной.
2. Какие из указанных прямых параллельны? у = 0,5х; у = - 0,5х; у = - 0,5х + 2. Почему?

Отгадай фамилию учёного:

Ключ к ответам

Кем был этот учёный, с чем связаны его работы, мы узнаем на следующем уроке.
Проверка ответов учащихся по карточкам.
IV Изучение нового материала.
Чтобы задать уравнение прямой на плоскости нам достаточно знать её угловой
коэффициент и координаты одной точки.

• Начнём с углового коэффициента

Рисунок 3

Рассмотрим график функции y = f(x) дифференцируемой в точке А (x 0 , f(x 0 )) .
Выберем на нём точку M (x 0 + Δх, f(x 0 + Δх)) и проведем секущую AM .
Вопрос: чему равен угловой коэффициент секущей? (∆f/∆x=tgβ)

Будем приближать по дуге точку M к точке A . В этом случае прямая AM будет поворачиваться вокруг точки A , приближаясь (для гладких линий) к некоторому предельному положению - прямой AT . Другими словами AT , обладающую таким свойством, называют касательной к графику функции y = f(x) в точке А(x 0 , f(x 0 )).

Угловой коэффициент секущей AM при AM → 0 стремится к угловому коэффициенту касательной AT Δf/Δx → f "(x 0 ) . Значение производной в точке х 0 примем за угловой коэффициент касательной. Говорят, что касательная есть предельное положение секущей при ∆х → 0 .

Существование производной функции в точке x 0 эквивалентно существованию (невертикальной) касательной в точке (x 0 , f(x 0 )) графика, при этом угловой коэффициент касательной равен f "(x 0 ) . В этом состоит геометрический смысл производной .

Определение касательной : Касательная к графику дифференцируемой в точке х 0 функции f - это прямая, проходящая через точку (x 0 , f(x 0 )) и имеющая угловой коэффициент f "(х 0 ) .
Проведем касательные к графику функции y = f(x) в точках х 1 , х 2 , х 3 , и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направлении от положительного направления оси до прямой.)

Рисунок 4

Мы видим, что угол α 1 острый, угол α 3 тупой, а угол α 2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого - отрицателен. Поэтому f "(х 1 )>0, f "(х 2 ) = 0, f "(х 3 )

• Выведем теперь уравнение касательной к графику функции f в точке А(x 0 , f(x 0 ) ).

Общий вид уравнения прямой y = kx + b .

1. Найдём угловой коэффициент k = f "(х 0 ), получим y = f "(х0)∙x + b, f(x) = f "(х 0 )∙x + b
2. Найдём b . b = f(x 0 ) - f "(х 0 )∙x 0 .
3. Подставим полученные значения k и b в уравнение прямой: y = f "(х 0 )∙x + f(x 0 ) - f "(х 0 )∙x 0 или y = f(x 0 ) + f "(х 0 )(x - x 0 )

• Обобщение материала лекции.

- сформулируйте алгоритм нахождения уравнения касательной в точке?

1. Значение функции в точке касания
2. Общую производную функции
3. Значение производной в точке касания
4. Подставить найденные значения в общее уравнение касательной.

V Закрепление изученного материала.

1. Устная работа:
1) В каких точках графика касательная к нему
а) горизонтальна;
б) образует с осью абсцисс острый угол;
в) образует с осью абсцисс тупой угол?
2) При каких значениях аргумента производная функции, заданной графиком
а) равна 0;
б) больше 0;
в) меньше 0?

3) На рисунке изображён график функции f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f "(x) в точке x 0 .

Рисунок 7

2. Письменная работа.
№ 253 (а, б), № 254 (а, б). (работа на местах, с комментарием)

3. Решение опорных задач.
Рассмотрим четыре типа задач. Дети читают условие задачи, предлагают алгоритм решения, один из учеников оформляет его на доске, остальные записывают в тетрадь.
1. Если задана точка касания
Составить уравнение касательной к графику функции f(x) = x 3 – 3x – 1 в точке М с абсциссой –2.
Решение:

1. Вычислим значение функции: f(-2) =(-2) 3 – 3(-2) – 1 = -3 ;
2. найдём производную функции: f "(х) = 3х 2 – 3;
3. вычислим значение производной: f "(-2) = - 9.;
4. подставим эти значения в уравнение касательной: y = 9(x + 2) – 3 = 9x + 15.

Ответ: y = 9x + 15.

2. По ординате точки касания.
Составить уравнение касательной в точке графика с ординатой y 0 = 1.
Решение:

Ответ: y = –x + 2 .

3. Заданного направления.
Написать уравнения касательной к графику y = x 3 – 2x + 7 , параллельной прямой у = х .
Решение.
Искомая касательная параллельна прямой y = x . Значит, они имеют один и тот же угловой коэффициент k = 1, y"(х) = 3х2 – 2. Абсцисса х 0 точек касания удовлетворяет уравнению 3х 2 – 2 = 1 , откуда х 0 = ±1.
Теперь можно написать уравнения касательных: y = x + 5 и y = x + 9 .
Ответ: y = x + 5 , y = x + 9 .

4. Условия касания графика и прямой.
Задача. При каких b прямая y = 0,5x + b является касательной к графику функции f(х) = ?
Решение.
Вспомним, что угловой коэффициент касательной – это значение производной в точке касания. Угловой коэффициент данной прямой равен k = 0,5. Отсюда получаем уравнение для определения абсциссы x точки касания: f "(х) = = 0,5. Очевидно, его единственный корень –х = 1. Значение данной функции в этой точке у(1) = 1. Итак, координаты точки касания (1; 1). Теперь остается подобрать такое значение параметра b, при котором прямая проходит через эту точку, то есть координаты точки удовлетворяют уравнению прямой: 1 = 0,5 ·1 + b, откуда b = 0,5.

5. Самостоятельная работа обучающего характера.

Работа в парах.


Проверка: результаты решения заносятся в таблицу на доске (от каждой пары один ответ), обсуждение ответов.

6. Нахождение угла пересечения графика функции и прямой.
Углом пересечения графика функции y = f(x) и прямой l называют угол, под которым в этой же точке прямую пересекает касательная к графику функции.
№ 259 (а, б), № 260 (а) – разобрать у доски.

7. Самостоятельная работа контролирующего характера. (работа дифференцированная, проверяет учитель к следующему уроку)
1 вариант.

2 вариант.

1. В каких точках касательная к графику функции f(x) = 3х 2 - 12х + 7 параллельна оси х?
2. Составьте уравнение касательной к графику функции f(x)= х 2 - 4 в точке с абсциссой х 0 = - 2. Выполните рисунок.
3. Выясните, является ли прямая у = 12х – 10 касательной к графику функции у = 4х 3 .

3 вариант.

VI Подведение итогов урока.
1. Ответы на вопросы
- что называется касательной к графику функции в точке?
- в чём заключается геометрический смысл производной?
- сформулируйте алгоритм нахождения уравнения касательной в точке?
2. Вспомните цели и задачи урока, достигли ли мы данной цели?
3. В чём были трудности на уроке, какие моменты урока наиболее понравились?
4. Выставление отметок за урок.
VII Комментарий домашнего задания: п. 19 (1, 2), № 253 (в), № 255 (г), № 256 (г), № 257 (г), № 259 (г). Подготовить сообщение о Лейбнице.

Литература

1. Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений. Составители:. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. - М.: Просвещение, 2008.

2. Дидактические материалы по алгебре и началам анализа для 10 класса / Б.М.Ивлев, С.М.Саакян, С.И. Шварцбурд. - М.: Просвещение, 2008.
3. Мультимедийный диск фирмы «1С». 1С: Репетитор. Математика (ч. 1) + Варианты ЕГЭ. 2006.
4. Открытый банк заданий по математике/ http://mathege.ru/